Základní obvody a zapojení číslicové techniky
Jelikož při nejmenším u některých mých obvodů je přímo vyžadována znalost základních obvodů a zapojení z číslicové techniky, rozhodl jsem se vytvořit stručný přehled toho nejzákladnějšího, s čím se můžete v mých zapojeních potýkat.
Předně bych rád ujasnil toto názvosloví, které běžně používám v mých návodech:
Logická nula = "0" = "L" = GND = zem
Logická jednička = "1" = "H" = Ucc = +5V
Logická nula se běžně používá pro aktivaci vstupů. To znamená, že chcete-li v mých obvodech třeba něco rozsvítit nebo potvrdit, musíte na příslušný vstup přivést právě hodnotu "0".
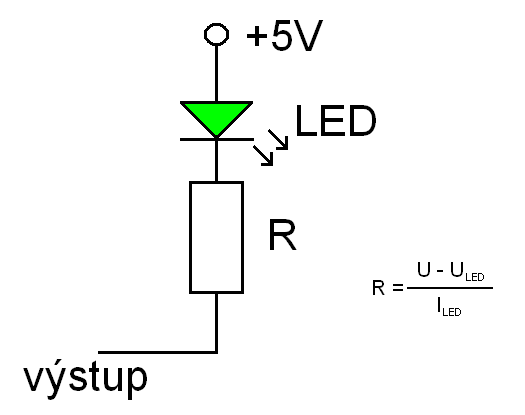
Za úplně nejzákladnější znalost považuji zapojení LED diod a tlačítek. Na následujícím obrázku můžete vidět, že nejběžnější zapojení LED diody je přivedení anody na +5V a katody na výstup přes rezistor. Hodnota tohoto rezistoru se vypočítá dle vzorce na obrázku. Odpor [Ohm] je roven celkovému napětí (5V) [V] mínus napětí na diodě [V] lomeno proudem [A]. Zde bych rád upozornil, že ne vždy je hodnota odporu určená výpočtem vyhovující. Pokud potřebujete, aby dioda svítila méně, stačí použít odpor s vyšší hodnotou. To nejčastěji využijete u bílé a možná modré LED diody, jejichž svítivost je skutečně vysoká. Pokud neznáte parametry diody, kterou máte zrovna po ruce, nemělo by vadit ani použití nějakého odporu v rozmezí +/- 330R až 1k5 a u bílé klidně i 10k.
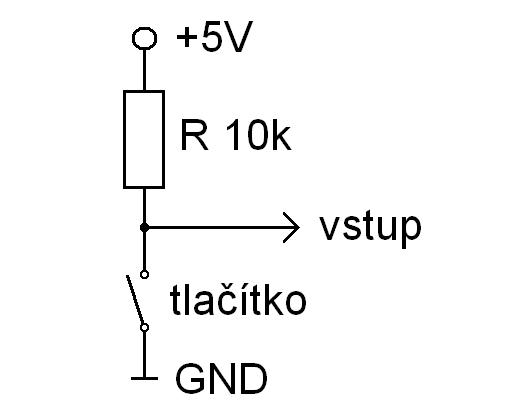
Pro zapojení tlačítek se nejčastěji využívá "tlačítek aktivních v logické nule". Tím je myšleno, že na vstup obvodu je trvale přiváděno napětí (zde vždy +5V) přes odpor s hodnotou 10k. Tlačítko je pak zapojeno proti zemi a jeho sepnutím se na vstup přivádí zem.
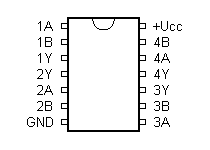
Dále bych zde ještě rád uvedl některé základní integrované obvody s jejich pravdivostními tabulkami a zapojením vývodů, bez kterých se možná neobejdete.
7404 - 6x NOT
Tento obvod se hodí poměrně často k negování signálů.
| A | Y |
| 0 | 1 |
| 1 | 0 |
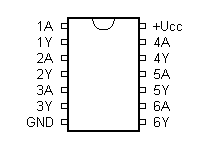
7408 - 4x 2-vstupý AND
Tento obvod využívám vždy, pokud chci realizovat podmínku "alespoň jeden ze vstupů je roven "0" ". Pro tuto podmínku lze mimo jiné rozšířit počet vstupů řazením jednotlivých hradel za sebe.
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
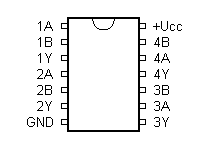
7432 - 4x 2-vstupý OR
Logický obvod OR využívám vždy, pokud chci realizovat podmínku "všechny vstupy jsou rovny "0" ". Pro tuto podmínku lze mimo jiné rozšířit počet vstupů řazením jednotlivých hradel za sebe.
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
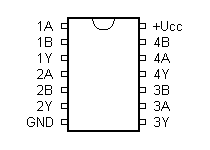
7400 - 4x 2-vstupý NAND
Jedná se asi o nejznámější logický obvod, se kterým se lze setkat.
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
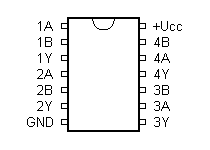
7402 - 4x 2-vstupý NOR
Tento obvod téměř nepoužívám.
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
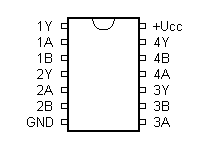
7486 - 4x 2-vstupý XOR
Tento obvod téměř nepoužívám.
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
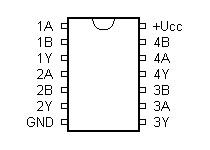
747266 - 4x 2-vstupý XNOR
Tento obvod téměř nepoužívám.
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |